Company formation in Lithuania
It is not complicated to open a company in Lithuania in the form of a limited liability company (SIA). Quite often, to open a business in Europe, start with the registration of the company and the opening of the enterprise in Lithuania, as compared to other EU countries, the costs of company formation in Lithuania and maintaining will be lower.

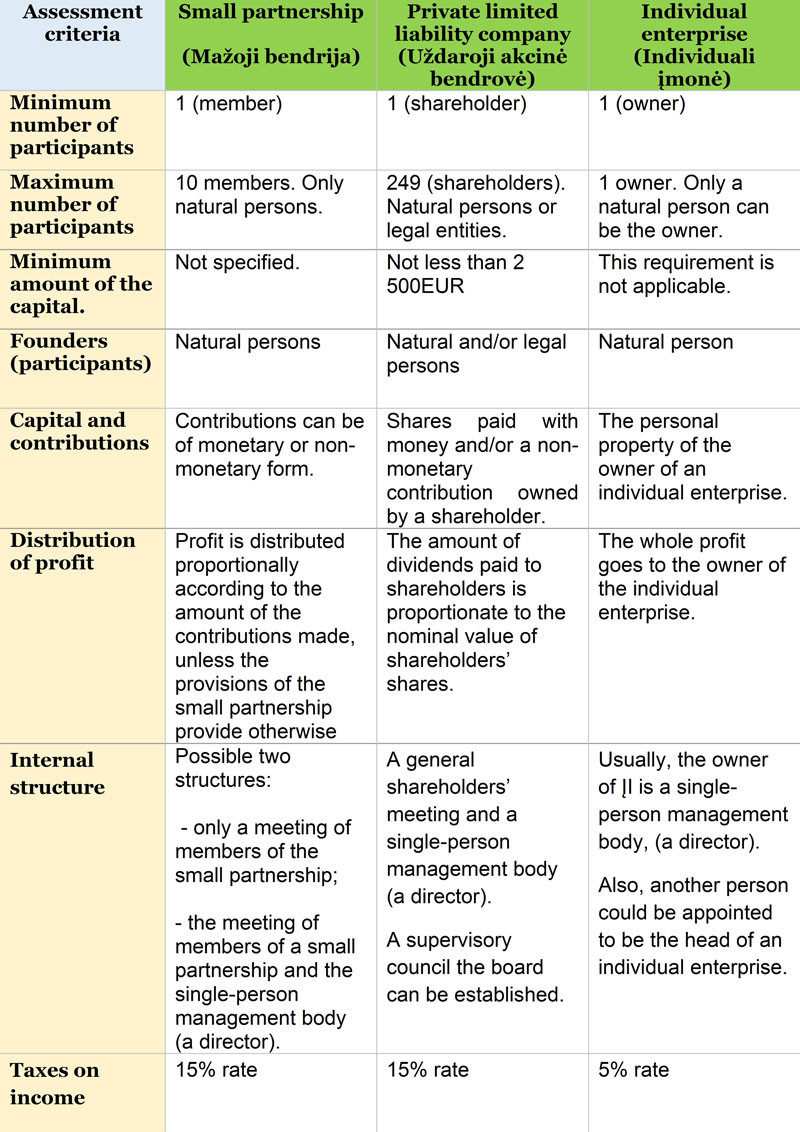
Types of companies in Lithuania
There are two types of limited liability companies (SIA) in Lithuania: (A) SIA with full capital (“ordinary” SIA). The minimum capital of the SIA with full capital is EUR 2,800, at least 50% of which must be paid before registration with temporary bank money; the rest is paid within one year of registration. (B) SIA with small capital. The capital stock of a small SIA is between EUR 1 and EUR 2,799, and it must be paid in full before registration. For SIA with small capital, there is no need to open a temporary bank account.

The main features of company formation in Lithuania

Documents/information required for the establishment of company in Lithuania.
To register a company in Lithuania it is necessary to prepare the constituent documents, which should contain the following information: information on the founders (natural persons): name, surname, valid passport number, date of issue and name of the body issuing the passport, personal code (if any), address of residence.

Accounting of the company in Lithuania
The company in Lithuania is obliged to submit monthly reports and pay taxes. Reports are filed even if there is no activity for some reason. On average, accounting services cost from €100 per month depending on the number of transactions conducted. At the customer’s request we provide the services of a qualified Russian-speaking accountant.

